پروژه: پیاده‌سازی الگوریتم FFT

شاید بتوان الگوریتم FFT را مهمترین الگوریتم ۱۰۰ سال اخیر در حوزه پردازش سیگنال دیجیتال دانست. الگوریتم FFT در بسیاری از سیستم‌های پردازش سیگنال کاربرد دارد و بنابراین، پیاده‌سازی بهینه آن، مساله مهمی در ساخت این نوع سیستم‌ها است. در این مقاله، در مورد این الگوریتم و نحوه پیاده‌سازی آن در FPGA صحبت خواهم کردم و ایده‌هایی را برای پیاده‌سازی ارائه خواهم کرد.

FFT چیست؟

الگوریتم FFT که مخفف عبارت Fast Fourier Transform است، یک روتین بسیار مناسب و بهینه برای پیاده‌سازی تبدیل DFT یا Discrete Fourier Transform است. اما در این لحظه ممکن است سوال کنید که DFT چیست؟

بر مبنای سری فوریه، می‌توان نشان داد که هر سیگنال پریودیک را می‌توان به صورت مجموع سیگنال‌های سینوسی و کسینوسی بیان کرد. به هر کدام از این سیگنال‌های سینوسی، یک مؤلفه گفته می‌شود. هر مؤلفه، یک فرکانس و دامنه دارد. بنابراین، اگر برای یک سیگنال یا موج در حوزه زمان، سری فوریه آن را محاسبه کنیم، می‌توان مؤلفه‌های آن را در نمودار دیگری که محور افقی آن فرکانس مؤلفه‌ها و محور عمودی آن، دامنه مؤلفه‌ها هستند نمایش داد. این نمایش را، نمایش حوزه فرکانس سیگنال می‌گویند.

مثلا فرض کنید سیگنال (x(t در حوزه زمان، دارای سری فوریه‌ زیر باشد:

(f(t) = a₁ sin(w₁t) + a₂ cos(w₂t) + a₃ sin(w₃t

یعنی این سیگنال دارای سه مؤلفه با فرکانس‌های w₁ ،w₂ و w₃ و دامنه‌های a_1 ،a₂ و a₃ است. نمایش حوزه فرکانس سیگنال (x(t در شکل زیر نشان داده شده است.

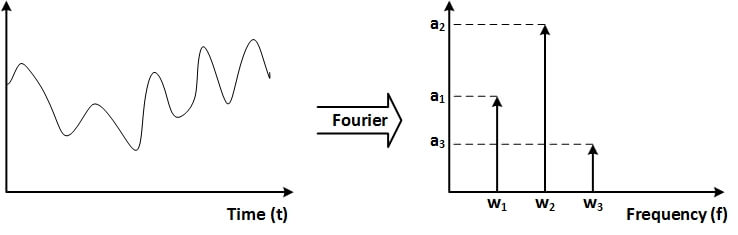
حال فرض کنید با یک سیگنال نمونه‌برداری شده (مثلا توسط یک مبدل آنالوگ به دیجیتال یا ADC) سروکار داریم. مثلا سیگنال (x(t در مثال فوق را با فرکانس F_s نمونه‌برداری کرده‌ایم. همچنین فرض کنید تعداد محدود و مشخصی از این نمونه‌ها را در اختیار داریم؛ مثلا تعداد N نمونه از سیگنال (x(t را با فرکانس F_s نمونه‌برداری کرده‌ایم.

الگوریتم DFT، الگوریتمی است که تعداد مشخصی از نمونه‌های گسسته یک سیگنال در حوزه زمان را که با فرکانس F_s نمونه‌برداری شده‌اند به عنوان ورودی دریافت می‌کند و در خروجی، ضرایب سری فوریه آن را محاسبه می‌کند. به عبارت دیگر، الگوریتم DFT، یک تابع گسسته را از حوزه زمان به حوزه فرکانس منتقل می‌کند. تعداد نمونه‌های در حوزه زمان ورودی (N) در این الگوریتم، با تعداد نمونه‌های حوزه فرکانس خروجی برابر است. مثلا در مورد مثال فوق، خروجی این الگوریتم برابر با دامنه‌های مؤلفه‌های سری فوریه، یعنی a₁ ،a₂ و a₃ خواهد بود. اگر تعداد ورودی‌های یک تبدیل DFT برابر با N باشد، به آن DFTی Nنقطه‌ای گفته می‌شود.

فاصله فرکانسی مؤلفه‌های محاسبه شده در خروجی DFT، برابر با F_s/N است. یعنی مثلا اگر از یک سیگنال در حوزه زمان با فرکانس نمونه‌برداری ۱۰۰MHz، تعداد ۱۰۰۰ نمونه توسط ADC تهیه شود و به الگوریتم DFT به عنوان ورودی اعمال شود، در خروجی این الگوریتم، ۱۰۰۰ نمونه در حوزه فرکانس خواهیم داشت که هر کدام از نمونه‌ها به اندازه ۱۰۰MHz/1000 = 100KHz با یکدیگر فاصله خواهند داشت. بنابراین، اولین خروجی DFT، مؤلفه فرکانس صفر است. دومین خروجی، مؤلفه فرکانس ۱۰۰KHz است. سومین مؤلفه خروجی DFT مربوط به فرکانس ۲۰۰KHz است و آخرین مؤلفه مربوط به فرکانس ۹۹۹۰۰KHz است.

شکل زیر، یک سیگنال فرضی در حوزه زمان را که با فرکانس ۱۰۰kHz نمونه‌برداری شده است به همراه تبدیل DFTی ۴نقطه‌ای آن که در حقیقت نمایش سیگنال در حوزه فرکانس است نشان می‌دهد. چون تعداد نقطه‌های DFT چهار عدد است و فرکانس نمونه‌برداری ۱۰۰kHz است، پس فاصله فرکانسی بین هر دو مؤلفه برابر با ۲۵kHz است.

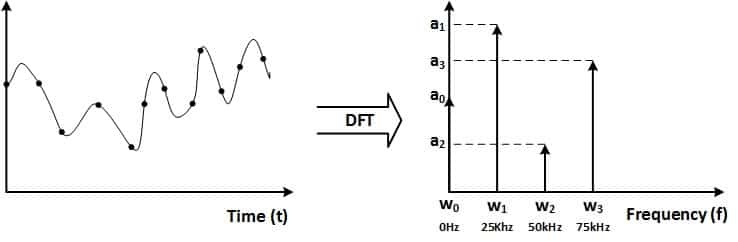
به این نکته هم توجه کنید که ورودی‌ها و خروجی‌های الگوریتم DFT، مختلط هستند. یعنی هر ورودی که یک نمونه در حوزه زمان است، به صورت x(n) = a + jb است و خروجی معادل آن هم به صورت F(n) = w + jz است. حال اگر شما سیگنالی نمونه‌برداری شده دارید که فقط شامل بخش‌های حقیقی است، می‌توانید مقدار بخش‌های موهومی را در ورودی DFT برابر با صفر قرار دهید. در هر حال، خروجی این تبدیل، هم شامل بخش حقیقی و هم شامل بخش موهومی خواهد بود. بنابراین، برای دستیابی به مؤلفه مورد نظر، باید مقدار دامنه خروجی مختلط، یعنی (sqrt(w^2 + z^2 را محاسبه کنید.

الگوریتم FFT، یک الگوریتم بهینه برای محاسبه سریع‌تر تبدیل DFT است. خروجی الگوریتم FFT همان مؤلفه‌های خروجی الگوریتم DFT است. اما الگوریتم FFT این کار را بسیار سریع‌تر انجام می‌دهد و شاید مهمتر از آن، دارای پیاده‌سازی بسیار ساده‌تری است.

الگوریتم FFT

رایج‌ترین الگوریتم پیاده‌سازی FFT در حال حاضر، الگوریتم Cooley–Tukey است. در این مقاله، قصد ندارم در مورد جزئیات این الگوریتم و محاسبات آن صحبت کنم و همچون مقالات قبلی، بیشتر در زمینه مباحث مربوط به پیاده‌سازی توضیح خواهد دادم.

برای اینکه با ساختار الگوریتم FFT برای پیاده‌سازی آشنا شوید، اجازه دهید یک FFTی چهار نقطه‌ای را با هم بررسی کنیم. در بخش بعدی، در مورد پیاده‌سازی این FFTی چهار نقطه‌ای ایده‌هایی به شما خواهم داد تا بتوانید به سرعت، پیاده‌سازی آن را شروع کنید. در بخش بعدی، توضیح خواهم داد که برای FFTهای بزرگ، بهتر است از IP Core یا ماجول‌های از پیش آماده شده استفاده کرد.

ساختار الگوریتم Cooley–Tukey ایجاب می‌کند که تعداد نمونه‌های FFT توانی از دو باشند. بنابراین، به کمک این الگوریتم می‌توان FFTهای ۴نقطه‌ای، ۸نقطه‌ای، …، ۱۰۲۴نقطه‌ای و … را پیاده‌سازی کرد. هسته اصلی در محاسبات الگوریتم FFT، بلوکی است به نام Butterfly که در شکل زیر نشان داده شده است. بلوک Butterfly در حقیقت یک FFTی دونقطه‌ای است که با اتصال مناسب تعدادی از آنها به یکدیگر می‌توان یک FFTی بزرگتر ایجاد کرد.

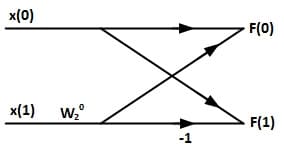
در بلوک Butterfly نشان داده شده در شکل بالا، (x(0 و (x(1 ورودی‌های مختلط و (F(0 و (F(1 خروجی‌های مختلط هستند. یک راه برای نمایش این ورودی‌ها و خروجی‌های مختلط، روش زیر است:

x(0) = x_{0_r} + jx_{0_i}

x(1) = x_{1_r} + jx_{1_i}

F(0) = F_{0_r} + jF_{0_i}

F(1) = F_{1_r} + jF_{1_i}

در شکل Butterfly روی بعضی از خط‌ها یک مقدار نوشته شده است که به این معنی است که ورودی باید در آن مقدار ضرب شود. در جاهایی که دو خط به یکدیگر رسیده‌اند، باید مقدار آن دو خط با یکدیگر جمع شوند. بنابراین، مقدار خروجی‌های Butterfly را می‌توان به صورت زیر نوشت:

(F(0) = x(0) + W₂⁰ x(1

(F(1) = x(0) – W₂⁰ x(1

ضریب W در این بلوک، خود دارای فرمول کلی e^(-j2πn/N) = W_Nⁿ است که در آن e^jx = cos x + j sin x است. در نتیجه ۱ = W₂⁰ است.

یک FFTی ۴نقطه‌ای از چهار بلوک Butterfly تشکیل شده است. شکل زیر، این FFT را نشان می‌دهد. همانطور که در شکل دیده می‌شود، در طبقه اول، دو بلوک Butterfly وجود دارد که خروجی آنها به نحو خاصی به دو Butterfly دیگر در طبقه دوم متصل شده است. همچنین دقت کنید که ورودی‌ها به ترتیب نرمال به بلوک‌های Butterfly متصل نشده‌اند. روش اتصال آنها را اصطلاحا بیت-معکوس یا bit-reverse می‌گویند.

در این مثال، سه ضریب W وجود دارد که با استفاده از فرمول فوق، مقدار آنها برابر خواهد بود با: ۱ = W₂⁰ = W₄⁰ و j = W₄^1_.

ایده‌هایی برای پیاده‌سازی فیلتر دیجیتال

پیاده‌سازی الگوریتم FFT خصوصا برای تعداد نقاط زیاد، کاری پیچیده و طولانی محسوب می‌شود و حتی در یک روند پیاده‌سازی حرفه‌ای نیز بهتر است از آن اجتناب شود. به همین دلیل، معمولا برای پیاده‌سازی FFT از IP Coreها که همان ماجول‌های از پیش‌آماده شده هستند استفاده می‌شود.

خوشبختانه در نرم‌افزار ISE، یک IP Core بسیار عالی برای پیاده‌سازی انواع FFT با تعداد نقاط مختلف و ساختارهای پیاده‌سازی متنوع وجود دارد که پیشنهاد می‌کنم در صورت نیاز به استفاده از این الگوریتم در پروژه‌تان، از این IP Core استفاده کنید.

اما در ادامه این مقاله و با هدف تمرین پیاده‌سازی و آشنایی با چند نکته مهم در پیاده‌سازی الگوریتم‌های با مقادیر مختلط، ایده‌هایی را برای پیاده‌سازی FFTی ۴نقطه‌ای ارائه خواهم داد. این پیاده‌سازی، یکی از تمرین‌های هفتگی دوره طراحی دیجیتال با FPGA در آموزشگاه فراد اندیش است و پیشنهاد می‌کنم شما هم حتما آن را پیاده‌سازی و تست کنید تا به کمک آن بتوانید مهارتتان را در پیاده‌سازی الگوریتم‌های پردازشی افزایش دهید.

مثل همیشه اجازه دهید ابتدا به سراغ تعیین ورودی‌ها و خروجی‌ها برویم. با توجه به اینکه می‌خواهیم یک FFTی ۴نقطه‌ای را پیاده‌سازی کنیم، نیاز به چهار ورودی و چهار خروجی خواهیم داشت. اما نکته‌ای که در این پروژه وجود دارد این است که ورودی‌ها و خروجی‌های FFT به صورت اعداد مختلط هستند و چیزی به نام پورت مختلط در زبان VHDL وجود ندارد.

برای تعریف پورت‌هایی که مربوط به اعداد مختلط می‌شوند باید به ازای هر ورودی یا خروجی، دو پورت تعریف کرد. یک پورت برای دریافت مقدار حقیقی و یک پورت برای دریافت مقدار موهومی. بنابراین، در این پروژه باید هشت پورت به عنوان ورودی و هشت پورت به عنوان خروجی تعریف کنیم. عرض بیت این پورت‌ها بستگی به مشخصات پروژه شما دارد. در این تمرین، من عرض بیت‌ها را هشت در نظر گرفته‌ام.

شکل زیر، ماجول FFTی ۴نقطه‌ای مختلط را برای پیاده‌سازی در FPGA نشان می‌دهد. برای پیاده‌سازی این FFT می‌توانید از یکی از دو ایده زیر پیروی کنید:

• نوشتن کد توصیف سخت‌افزاری این FFT به صورت یک ماجول؛
• نوشتن ماجول Butterfly و سپس اتصال چهار نمونه از ماجول Butterfly در یک ماجول دیگر.

همچنین در پیاده‌سازی به هر کدام از دو روش فوق، می‌توانید از تکنیک پایپ‌لاین برای افزایش سرعت کلاک قابل اعمال به ماجول استفاده کنید.

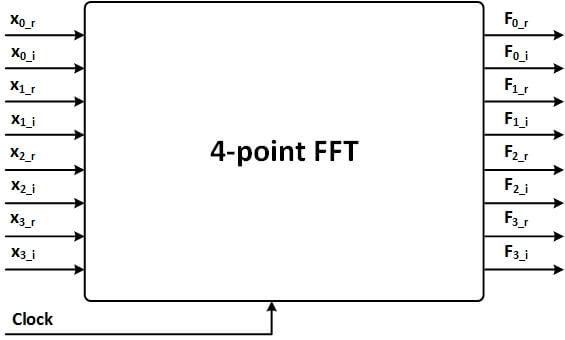
در پیاده‌سازی بسیاری از الگوریتم‌ها از جمله الگوریتم این پروژه، بهتر است ابتدا و قبل از شروع پیاده‌سازی، بخشی از محاسبات را روی کاغذ انجام دهید و سپس عبارات محاسباتی ساده شده را پیاده‌سازی کنید. اجازه دهید ابتدا یک بلوک Butterfly را پیاده‌سازی کنیم.

ارتباط بین ورودی‌ها و خروجی‌های بلوک Butterfly به صورت تعریف می‌شود:

(F(0) = x(0) + W₂⁰ x(1

(F(1) = x(0) – W₂⁰ x(1

اگر به جای (F(nها، (x(nها و W_Nⁿها مقدار مختلط آنها را از روابطی که بالاتر به آنها اشاره کردم قرار دهیم، عبارات زیر به دست خواهند آمد:

(F(0) = (x_{0_r} + x_{1_r}) + j(x_{0_i} + x_{1_i}

(F(1) = (x_{0_r} – x_{1_r}) + j(x_{0_i} – x_{1_i}

و چون خود (F(nها مختلط هستند داریم:

F(0) = F_{0_r} + jF_{0_i}

F(1) = F_{1_r} + jF_{1_i}

در نتیجه داریم:

F_{0_r} = x_{0_r} + x_{1_r}

F_{0_i} = x_{0_i} + x_{1_i}

F_{1_r} = x_{0_r} – x_{1_r}

F_{1_i} = x_{0_i} – x_{1_i}

بنابراین، چهار خروجی بلوک Butterfly را می‌توان از طریق روابط فوق محاسبه کرد.

همانطور که پیش‌تر هم اشاره کردم، در این مرحله می‌توانید دو ایده را در نظر بگیرید. ایده اول این است که به کمک چهار بلوک Butterfly که در بالا طراحی کردیم و اتصال مناسب آنها به یکدیگر در ماجول اصلی (ماجول FFTی ۴نقطه‌ای) طراحی را کامل کنیم.

ایده دوم هم این است که کل محاسبات مربوط به FFTی ۴نقطه‌ای را مشابه کاری که برای بلوک Butterfly انجام دادیم، کامل کنیم و FFT را در یک ماجول پیاده‌سازی کنیم. پیشنهاد می‌کنم شما هر دو روش را انجام دهید و نتیجه را با یکدیگر مقایسه کنید.

در انجام این پروژه در نظر داشته باشید که نیاز به هیچ عمل ضربی ندارید. چون مقادیر W_Nⁿها در این تمرین خاص، برابر با ۱، ۱- یا j- است و برای هیچکدام از این موارد نیاز نیست که از عملگر ضرب استفاده شود. همانطور که می‌دانید، اگر عدد مختلطی در j- ضرب شود، فقط جای مقدار حقیقی با موهومی عوض می‌شود و مقدار حقیقی حاصل هم تغییر علامت می‌دهد.

قدم بعدی برای پیاده‌سازی الگوریتم FFT

با توجه به اینکه در عمل، FFTی ۴نقطه‌ای کاربردی ندارد و پیاده‌سازی FFTهای بزرگ‌تر هم معمولا به کمک IP Coreها انجام می‌شود، پیشنهاد می‌کنم یک ماجول FFTی ۱۲۸نقطه‌ای را به کمک IP Core موجود در نرم‌افزار ISE پیاده‌سازی کنید.

بعد از انتخاب IP Core، باید تنظیمات مختلفی را برای IP انجام دهید. مثلا تعداد نقاط FFT و عرض بیت‌ها را مشخص کنید. تنظمیات دیگری هم وجود دارند که می‌توانید با مطالعه Datasheet این IP که در نرم‌افزار موجود است، آنها را به نحو مناسب انجام دهید.

به زودی کارگاهی را در زمینه پیاده‌سازی الگوریتم‌های پردازش سیگنال با FPGA برگزار خواهم کردم که در آن به اصول و روش‌های پیاده‌سازی انواع الگوریتم‌های پردازش سیگنال به کمک FPGA خواهم پرداخت. به کمک اطلاعاتی که از این کارگاه به دست خواهید آورد، می‌توانید دانش و مهارت خودتان را در بکارگیری FPGAها برای طراحی مدارات دیجیتال، یک گام به جلو ببرید و قابلیت خودتان را در انجام پروژه‌های حرفه‌ای و بزرگ به نحو چشمگیری افزایش دهید.

چطور از صحت پیاده‌سازی خودمان مطمئن شویم؟

بعد از پیاده‌سازی FFTی ۴نقطه‌ای، می‌توانید به کمک تست‌بنچ آن را شبیه‌سازی کنید. برای اینکه بتوانید خروجی‌های ماجول خودتان را با یک مقدار درست مقایسه کنید، بهتر است از نرم‌افزار MATLAB استقاده کنید. چهار مقدار مختلط دلخواه را به عنوان ورودی انتخاب کنید و توسط تابع fft در نرم‌افزار MATLAB مقدار آن را محاسبه کنید. برای این کار می‌توانید در نرم‌افزار MATLAB بنویسید:

[x = [7+i 5-4i 3+23i 9-2i

(fft(x

جوابی که در نرم‌افزار مشاهده خواهید کرد به صورت زیر خواهد بود:

۲۴+۱۸i 2-18i -4+30i 6-26i

حال می‌توانید در تست‌بنچ، مقادیر ورودی را به پورت‌های ورودی مدار اعمال کنید و شبیه‌سازی را انجام دهید. درنرم‌افزار شبیه‌ساز ISim باید همان خروجی‌های محاسبه شده در نرم‌افزار MATLAB را مشاهده کنید.

آیا پروژه پیاده‌سازی الگوریتم FFT برای شما مفید بود؟